WEDNESDAY, OCT 31, 2018 or 21iX68
Federation Calendar
From Wikipedia article accessed 35V403 (June 23, 2353)
via Wayforward Machine
Eric Lee, A-SOCIATED PRESS
TOPICS: FEDERATION CALENDAR, FROM THE WIRES, TIME ENOUGH
Abstract: When complex societies are working, reforms are difficult to enact. When rebuilding post-collapse, however, changes that make sense may be embraced. Calendar reform is a perennial favorite of reformers, so with the coming of the United Federation of Watersheds global management SYSTEM, that sought to minimize temporal blindness (lacking temporal causal cohesion), came temporal reforms.
TUCSON (A-P) — The modern calendar was invented by Ms. Wong's fifth-grade math class in 142 AA and adopted in 144 AA following peer review by the newly formed Federation Academy of Evidence and Reason.
The new year starts the day after the winter solstice in the Northern hemisphere or summer solstice in the Southern hemisphere. The solstice is the last day of the year which always falls on 36X. The first leap day L1, New Year's day, is followed by the other leap days, New Year's day L2, L3, L4, L5, and mostly every four years by L6 with an extra L6 added between leap years every four hundred years as needed. The five (sometimes six) leap days of New Year, together with the solstice (as L0) total six or seven days of Gaia Festival each Earth orbit.
Months are written using Roman numerals and spoken using the Latin name or abbreviation. The next day following the last leap day begins the first month i (Un), with days 1i (1 Un) to 36i (36 Un), followed by month ii (Duo), days 1ii to 36ii (1 Duo to 36 Duo), then month iii (Tres), and days 1iii to 36iii, then iV (Quat), with days 1iV to 36iV, then V (Quin), days 1V to 36V, then Vi (Sex), days 1Vi to 36Vi, then Vii (Sept), days 1Vii to 36Vii, then Viii (Oct), days 1Viii to 36Viii, then iX (Nov), days 1iX to 36iX, then X (Dec), days 1X to 36X (1 Dec to 36 Dec). [Note: To better distinguish the number 1 from uppercase 'I' from lowercase 'l', in Roman numerals a lowercase 'i' is used instead of capital I, as was suggested by Bobby Smith of Ms. Wong's class, whom the other students thought was backward, who also suggested 12 months of 30 days each.]
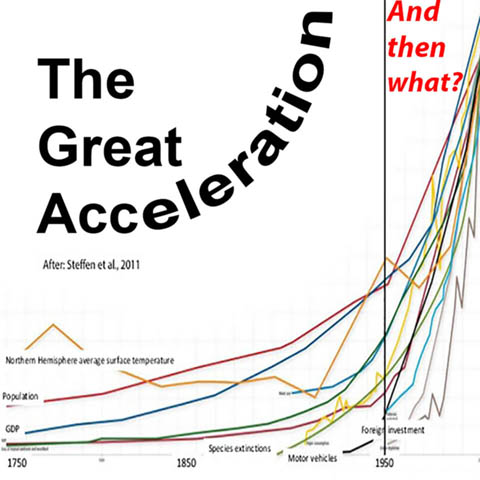Years are numbered starting from 0 AA (After Acceleration is defined as beginning in 1950 CE, so 2001 CE = 51 AA). The beginning is the Great Acceleration of 1950, the turning point of the Anthropocene (June 1950, six months into the Great Acceleration, would be year 0 AA, plus 6 months with 1951 being the first year AA). Year 1 CE of the Gregorian calendar is 1949 BA (Before Acceleration), and 1 BCE is 1950 BA (or BP).
To convert from CE to BA: |1950-CE| = BA, and to convert from BCE to BA: BCE + 1949 = BA, so Euro-Sino Empire calendar day December 21, 2018 CE is Federation calendar date 36X68 (or L069) and December 22, 2018 is L169, where AA is implied for years after 1950 CE. The current year (2353 CE per prior calendar) ends on the Northern hemisphere's winter solstice in 36X403, so December 21, 1821 CE is 36X129 BA [and October 31, 2018 CE is 21iX68 (or spoken: 21 Nov 68)].
Once it was clear that technology-enabled humans were responsible for a new epoch, the question of when the Anthropocene started was argued for decades with some arguing for Homo erectus' use of fire technology to alter landscapes as the beginning, Or was it the megafauna extinctions on every continent as Homo sapiens left Africa to become an invasive species? Or was it agriculture empowered empire-building? Or the start of the Industrial Revolution? Or was it the first atomic blast whose radioactive fallout would leave a trace in the geological record to mark the beginning? A consensus arose within the Federation Academy, however, that the beginning was of less significance that the turning point when the slope of the averaged exponential growth curves exceeded 45 degrees, the point when acceleration kicked in, which was very close to 1950 CE that also marked the "present" in BP (Before Present) so converting BP to BA just involves changing the "P" to "A". That geometric growth was unsustainable had been considered by a few since 152 BA, but until 1950 CE such growth seemed theoretical. In the short term it seemed like the best thing that could possibly happen to humanity, and it was, but very few could ask, "And then what?" No one could understand the exponential function and serve the SYSTEM with enthusiasm, and so such understanding was strongly selected against, as those who did understand the implications often self-selected out of the growth hegemon and failed to "prosper".
The 36 day month can be divided into 2, 3, 4, 6, 9, 12, and 18 day cycles or weeks that repeat regularly throughout the year other than during the New Year's Festival. Diurnal time similarly benefits from the 36 hour day of 100 minutes per hour. To convert pre-Fed time:
Fed Time vs Euro-Sino Time
36 hours = 24 hours (1 day)
1.5 hours = 1 hour
1 hour = 0.667 hours
1 hour = 40 minutes
1 minute = 0.4 minutes
1 minute = 24 seconds
1 second = 0.24 seconds
150 minutes = 1 hour
250 seconds = 1 minute
One month of 36 days:
6 weeks of 6 day weeks:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 |
2 weeks of 18 days:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
3 weeks of 12 days:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
4 weeks of 9 days:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
9 weeks of 4 days:
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 |
| 29 | 30 | 31 | 32 |
| 33 | 34 | 35 | 36 |
12 weeks of 3 days:
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| 10 | 11 | 12 |
| 13 | 14 | 15 |
| 16 | 17 | 18 |
| 19 | 20 | 21 |
| 22 | 23 | 24 |
| 25 | 26 | 27 |
| 28 | 29 | 30 |
| 31 | 32 | 33 |
| 34 | 35 | 36 |
18 weeks of 2 days:
| 1 | 2 |
| 3 | 4 |
| 5 | 6 |
| 7 | 8 |
| 9 | 10 |
| 11 | 12 |
| 13 | 14 |
| 15 | 16 |
| 17 | 18 |
| 19 | 20 |
| 21 | 22 |
| 23 | 24 |
| 25 | 26 |
| 27 | 28 |
| 29 | 30 |
| 31 | 32 |
| 33 | 34 |
| 35 | 36 |
In the Gregorian calendar there is only one seven-day week with each day having a proper name, Monday being first and Sunday being the last. Once the Judeo-Christian-Islamic hegemon became of largely historical interest, humans were able to consider non-seven-day patterns and one agruement for the calendar was that it lacked a seven-day cycle. But there is seven cycles in a month, so everyone ended up happy.
In the Federation calendar the day in the week (1 thru 9 in a nine-day week) is followed by the cycle # (1-4 if four weeks of nine days) times the total numbers of days in the week (2, 3, 4, 6, 9, 12, or 18). So 1+2x9 is the first day of the second week of the four-week month or day (1+1x9=) 10 of the month, and 2+3x9 is the second day of the third week of four or day (2+2x9=) 20 of the month. Federation educated children quickly interpret days of the week, so "13+2x18" is understood to be the 13th day of the second week of the 18-days per 2 week cycle or day (13+1x18=) 31 of the month..
Each 360 day period can be divided into repeating cycles:
| 180 | 2-day cycles |
| 120 | 3-day cycles |
| 90 | 4-day cycles |
| 60 | 6-day cycles |
| 40 | 9-day cycles |
| 36 | 10-day cycles |
| 30 | 12-day cycles |
| 20 | 18-day cycles |
| 18 | 20-day cycles |
| 12 | 30-day cycles |
| 10 | 36-day cycles |
| 9 | 40-day cycles |
| 6 | 60-day cycles |
| 4 | 90-day cycles |
| 3 | 120-day cycles |
| 2 | 180-day cycles |
The concept of a year and a day is defined by the sun. The Federation Calendar maximizes the number of possible cycles at the cost of an annual festival when cycles take a break (some humans, e.g. nurses, won't get the entire festival off, but otherwise, per Federation custom, all businesses/organizations/services/machinery that can stop do, and people celebrate having enough to consume without relying on others, including energy slaves, ,so by tradition no electrical services are used, including lighting, when possible).
The concept of month and week could be replaced by cycle, as in 'what day of the cycle is it?' If referring to 10 cycles/year of 36 days/cycle, then there are three questions: What day of the cycle is it; what cycle is it; and how many days per cycle? So 3+2x36 means 3rd day of second cycle of 36-day cycle. So (day plus cycle# minus 1)xdays in cycle = day of year. So for 180+2x180, the 180th day of second and last cycle of 180 days is (180+1x180) or the 360th day of the year. Today is the end of the year, 36X, or L0, and tomorrow is L1.
By convention, for cycles of 18 or fewer days, the cycle refers to a monthly cycle, while over 18 refers to annual cycles. So 12+4x90 refers to the 12th day of the fourth quarter (360/90) of the year, which would be the day (12+3x90) 282 of the year.
Federation Day of Year and Gregorian Day
L0=12/21 (aka 36X)
L1=12/22
L2=12/23
L3=12/24
L4=12/25
L5=12/26
L6=12/27 (leap years only)
Non-Leap Years:
| 1i=12/27 | 1ii=2/1 | 1iii=3/9 | 1iV=4/14 | 1V=5/20 | 1Vi=6/25 | 1Vii=7/31 | 1Viii=9/5 | 1iX=10/11 | 1X=11/16 |
| 2i=12/28 | 2ii=2/2 | 2iii=3/10 | 2iV=4/15 | 2V=5/21 | 2Vi=6/26 | 2Vii=8/1 | 2Viii=9/6 | 2iX=10/12 | 2X=11/17 |
| 3i=12/29 | 3ii=2/3 | 3iii=3/11 | 3iV=4/16 | 3V=5/22 | 3Vi=6/27 | 3Vii=8/2 | 3Viii=9/7 | 3iX=10/13 | 3X=11/18 |
| 4i=12/30 | 4ii=2/4 | 4iii=3/12 | 4iV=4/17 | 4V=5/23 | 4Vi=6/28 | 4Vii=8/3 | 4Viii=9/8 | 4iX=10/14 | 4X=11/19 |
| 5i=12/31 | 5ii=2/5 | 5iii=3/13 | 5iV=4/18 | 5V=5/24 | 5Vi=6/29 | 5Vii=8/4 | 5Viii=9/9 | 5iX=10/15 | 5X=11/20 |
| 6i=1/1 | 6ii=2/6 | 6iii=3/14 | 6iV=4/19 | 6V=5/25 | 6Vi=6/30 | 6Vii=8/5 | 6Viii=9/10 | 6iX=10/16 | 6X=11/21 |
| 7i=1/2 | 7ii=2/7 | 7iii=3/15 | 7iV=4/20 | 7V=5/26 | 7Vi=7/1 | 7Vii=8/6 | 7Viii=9/11 | 7iX=10/17 | 7X=11/22 |
| 8i=1/3 | 8ii=2/8 | 8iii=3/16 | 8iV=4/21 | 8V=5/27 | 8Vi=7/2 | 8Vii=8/7 | 8Viii=9/12 | 8iX=10/18 | 8X=11/23 |
| 9i=1/4 | 9ii=2/9 | 9iii=3/17 | 9iV=4/22 | 9V=5/28 | 9Vi=7/3 | 9Vii=8/8 | 9Viii=9/13 | 9iX=10/19 | 9X=11/24 |
| 10i=1/5 | 10ii=2/10 | 10iii=3/18 | 10iV=4/23 | 10V=5/29 | 10Vi=7/4 | 10Vii=8/9 | 10Viii=9/14 | 10iX=10/20 | 10X=11/25 |
| 11i=1/6 | 11ii=2/11 | 11iii=3/19 | 11iV=4/24 | 11V=5/30 | 11Vi=7/5 | 11Vii=8/10 | 11Viii=9/15 | 11iX=10/21 | 11X=11/26 |
| 12i=1/7 | 12ii=2/12 | 12iii=3/20 | 12iV=4/25 | 12V=5/31 | 12Vi=7/6 | 12Vii=8/11 | 12Viii=9/16 | 12iX=10/22 | 12X=11/27 |
| 13i=1/8 | 13ii=2/13 | 13iii=3/21 | 13iV=4/26 | 13V=6/1 | 13Vi=7/7 | 13Vii=8/12 | 13Viii=9/17 | 13iX=10/23 | 13X=11/28 |
| 14i=1/9 | 14ii=2/14 | 14iii=3/22 | 14iV=4/27 | 14V=6/2 | 14Vi=7/8 | 14Vii=8/13 | 14Viii=9/18 | 14iX=10/24 | 14X=11/29 |
| 15i=1/10 | 15ii=2/15 | 15iii=3/23 | 15iV=4/28 | 15V=6/3 | 15Vi=7/9 | 15Vii=8/14 | 15Viii=9/19 | 15iX=10/26 | 15X=11/30 |
| 16i=1/11 | 16ii=2/16 | 16iii=3/24 | 16iV=4/29 | 16V=6/4 | 16Vi=7/10 | 16Vii=8/15 | 16Viii=9/20 | 16iX=10/26 | 16X=12/1 |
| 17i=1/12 | 17ii=2/17 | 17iii=3/25 | 17iV=4/30 | 17V=6/5 | 17Vi=7/11 | 17Vii=8/16 | 17Viii=9/21 | 17iX=10/27 | 17X=12/2 |
| 18i=1/13 | 18ii=2/18 | 18iii=3/26 | 18iV=5/1 | 18V=6/6 | 18Vi=7/12 | 18Vii=8/17 | 18Viii=9/22 | 18iX=10/28 | 18X=12/3 |
| 19i=1/14 | 19ii=2/19 | 19iii=3/27 | 19iV=5/2 | 19V=6/7 | 19Vi=7/13 | 19Vii=8/17 | 19Viii=9/23 | 19iX=10/29 | 19X=12/4 |
| 20i=1/15 | 20ii=2/20 | 20iii=3/28 | 20iV=5/3 | 20V=6/8 | 20Vi=7/14 | 20Vii=8/19 | 20Viii=9/24 | 20iX=10/30 | 20X=12/5 |
| 21i=1/16 | 21ii=2/21 | 21iii=3/29 | 21iV=5/4 | 21V=6/9 | 21Vi=7/15 | 21Vii=8/20 | 21Viii=9/25 | 21iX=10/31 | 21X=12/6 |
| 22i=1/17 | 22ii=2/22 | 22iii=3/30 | 22iV=5/5 | 22V=6/10 | 22Vi=7/16 | 22Vii=8/21 | 22Viii=9/26 | 22iX=11/1 | 22X=12/7 |
| 23i=1/18 | 23ii=2/23 | 23iii=3/31 | 23iV=5/6 | 23V=6/11 | 23Vi=7/17 | 23Vii=8/22 | 23Viii=9/27 | 23iX=11/2 | 23X=12/8 |
| 24i=1/19 | 24ii=2/24 | 24iii=4/1 | 24iV=5/7 | 24V=6/12 | 24Vi=7/18 | 24Vii=8/23 | 24Viii=9/28 | 24iX=11/3 | 24X=12/9 |
| 25i=1/20 | 25ii=2/25 | 25iii=4/2 | 25iV=5/8 | 25V=6/13 | 25Vi=7/19 | 25Vii=8/24 | 25Viii=9/29 | 25iX=11/4 | 25X=12/10 |
| 26i=1/21 | 26ii=2/26 | 26iii=4/3 | 26iV=5/9 | 26V=6/14 | 26Vi=7/20 | 26Vii=8/25 | 26Viii=9/30 | 26iX=11/5 | 26X=12/11 |
| 27i=1/22 | 27ii=2/27 | 27iii=4/4 | 27iV=5/10 | 27V=6/15 | 27Vi=7/21 | 27Vii=8/26 | 27Viii=10/1 | 27iX=11/6 | 27X=12/12 |
| 28i=1/23 | 28ii=2/28 | 28iii=4/5 | 28iV=5/11 | 28V=6/16 | 28Vi=7/22 | 28Vii=8/27 | 28Viii=10/2 | 28iX=11/7 | 28X=12/13 |
| 29i=1/24 | 29ii=3/1 | 29iii=4/6 | 29iV=5/12 | 29V=6/17 | 29Vi=7/23 | 29Vii=8/28 | 29Viii=10/3 | 29iX=11/8 | 29X=12/14 |
| 30i=1/25 | 30ii=3/2 | 30iii=4/7 | 30iV=5/13 | 30V=6/18 | 30Vi=7/24 | 30Vii=8/29 | 30Viii=10/4 | 30iX=11/9 | 30X=12/15 |
| 31i=1/26 | 31ii=3/3 | 31iii=4/8 | 31iV=5/14 | 31V=6/19 | 31Vi=7/25 | 31Vii=8/30 | 31Viii=10/5 | 31iX=11/10 | 31X=12/16 |
| 32i=1/27 | 32ii=3/4 | 32iii=4/9 | 32iV=5/15 | 32V=6/20 | 32Vi=7/26 | 32Vii=8/31 | 32Viii=10/6 | 32iX=11/11 | 32X=12/17 |
| 33i=1/28 | 33ii=3/5 | 33iii=4/10 | 33iV=5/16 | 33V=6/21 | 33Vi=7/27 | 33Vii=9/1 | 33Viii=10/7 | 33iX=11/12 | 33X=12/18 |
| 34i=1/29 | 34ii=3/6 | 34iii=4/11 | 34iV=5/17 | 34V=6/22 | 34Vi=7/28 | 34Vii=9/2 | 34Viii=10/8 | 34iX=11/13 | 34X=12/19 |
| 35i=1/30 | 35ii=3/7 | 35iii=4/12 | 35iV=5/18 | 35V=6/23 | 35Vi=7/29 | 35Vii=9/3 | 35Viii=10/9 | 35iX=11/14 | 35X=12/20 |
| 36i=1/31 | 36ii=3/8 | 36iii=4/13 | 36iV=5/19 | 36V=6/24 | 36Vi=7/30 | 36Vii=9/4 | 36Viii=10/10 | 36iX=11/15 | 36X=12/21 |
Leap Years
Except for the first month and part of the second, the dates are the same:
L6=12/27
| 1i=12/28 | 1ii=2/2 |
| 2i=12/29 | 2ii=2/3 |
| 3i=12/30 | 3ii=2/4 |
| 4i=12/31 | 4ii=2/5 |
| 5i=1/1 | 5ii=2/6 |
| 6i=1/2 | 6ii=2/7 |
| 7i=1/3 | 7ii=2/8 |
| 8i=1/4 | 8ii=2/9 |
| 9i=1/5 | 9ii=2/10 |
| 10i=1/6 | 10ii=2/11 |
| 11i=1/7 | 11ii=2/12 |
| 12i=1/8 | 12ii=2/13 |
| 13i=1/9 | 13ii=2/14 |
| 14i=1/10 | 14ii=2/15 |
| 15i=1/11 | 15ii=2/16 |
| 16i=1/12 | 16ii=2/17 |
| 17i=1/13 | 17ii=2/18 |
| 18i=1/14 | 18ii=2/19 |
| 19i=1/15 | 19ii=2/20 |
| 20i=1/16 | 20ii=2/21 |
| 21i=1/17 | 21ii=2/22 |
| 22i=1/18 | 22ii=2/23 |
| 23i=1/19 | 23ii=2/24 |
| 24i=1/20 | 24ii=2/25 |
| 25i=1/21 | 25ii=2/26 |
| 26i=1/22 | 26ii=2/27 |
| 27i=1/23 | 27ii=2/28 |
| 28i=1/24 | 28ii=2/29 |
| 29i=1/25 | 29ii=3/1 |
| 30i=1/26 | 31ii=3/2 |
| 31i=1/27 | 32ii=3/3 |
| 32i=1/28 | 33ii=3/4 |
| 33i=1/29 | 34ii=3/5 |
| 34i=1/30 | 35ii=3/6 |
| 35i=1/31 | 36ii=3/7 |
| 36i=2/1 | 36ii=3/8 |
As in the Gregorian calendar three criteria must be taken into account to identify leap years:
- The year BA or AA can be evenly divided by 4;
- If the year can be evenly divided by 100, it is NOT a leap year, unless;
- The year is also evenly divisible by 400. Then it is a leap year.
So 1948 CE (2BA) was a leap year, so to convert CE to BA to the day, allow for the extra leap day for BA-2 leap years. Year 4 (AA) was a leap year, but 1954 CE was not. For AA-2 leap years, the CE year was a leap year. The year 402 (2352 CE) was an extra leap year.
